FractalGiới thiệu

Khi nhìn xung quanh thiên nhiên, bạn có thể nhận thấy những loài thực vật phức tạp như thế này:

Dương xỉ này bao gồm nhiều lá nhỏ phân nhánh lớn hơn.

Romanesco bông cải xanh này bao gồm các hình nón xoắn ốc xung quanh một cái lớn hơn.

Ban đầu, chúng có hình dạng rất phức tạp - nhưng khi bạn nhìn gần hơn, bạn có thể nhận thấy rằng cả hai đều theo một mô hình tương đối đơn giản: tất cả các bộ phận riêng lẻ của các cây trông giống hệt như toàn bộ Cây, chỉ nhỏ hơn. Mô hình tương tự được lặp đi lặp lại nhiều lần, ở quy mô nhỏ hơn.

Trong toán học, chúng ta gọi thuộc tính này là tự tương tự và các hình dạng có tên đó là fractals. Chúng là một trong những vật thể đẹp nhất và kỳ quái nhất trong tất cả toán học.

Để tạo ra các hình nhỏ của riêng mình, chúng ta phải bắt đầu với một mẫu đơn giản và sau đó lặp đi lặp lại nhiều lần, ở quy mô nhỏ hơn.

Một trong những mẫu đơn giản nhất có thể là phân đoạn dòng , với hai phân đoạn nữa phân nhánh một đầu. Nếu chúng ta lặp lại mô hình này, cả hai phân đoạn màu xanh này cũng sẽ có thêm hai nhánh ở cuối của chúng.

Bạn có thể di chuyển dấu chấm màu xanh để thay đổi độ dài và góc của tất cả các nhánh. Sau đó tăng số lần lặp bằng cách sử dụng thanh trượt bên dưới.

Tùy thuộc vào vị trí của các nhánh, bạn có thể tạo các mẫu hoàn toàn khác nhau - trông giống như ở trên, một hoặc . Bạn có thể tìm thấy gì khác?

Một fractal nổi tiếng khác là tam giác Sierpinki. Trong trường hợp này, chúng ta bắt đầu với một hình tam giác lớn, bằng nhau, và sau đó liên tục cắt các hình tam giác nhỏ hơn ra khỏi các phần còn lại.

Lưu ý cách hình dạng cuối cùng được tạo thành từ ba bản sao giống hệt nhau của chính nó và mỗi bản sao này được tạo thành từ các bản sao nhỏ hơn của toàn bộ tam giác! Bạn có thể tiếp tục phóng to vào hình tam giác mãi mãi, và các mẫu và hình dạng sẽ luôn tiếp tục lặp lại.

Các nhà máy ở đầu chương này trông giống như các fractals, nhưng rõ ràng không thể tạo ra các fractals thật trong đời thực. Nếu chúng ta cứ lặp đi lặp lại cùng một kiểu lặp đi lặp lại, nhỏ hơn và nhỏ hơn, cuối cùng chúng ta sẽ đến được các tế bào, phân tử hoặc nguyên tử không còn có thể phân chia được nữa.

Tuy nhiên, bằng cách sử dụng toán học, chúng ta có thể nghĩ về các thuộc tính mà fractals thực sự sẽ có - và đây là những điều rất đáng ngạc nhiên

Kích thước Fractal

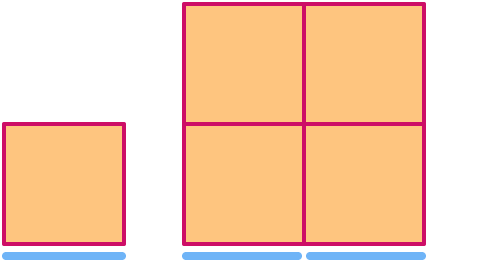
Đầu tiên, hãy để ý nghĩ về kích thước của fractals. Một dòng có thứ nguyên . Khi nhân rộng nó theo hệ số 2, chiều dài của nó tăng theo hệ số 21=2. Rõ ràng!

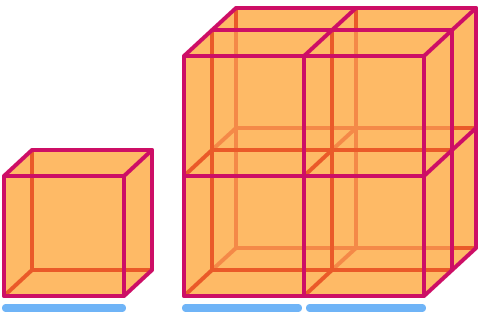
Một hình vuông có kích thước . Khi nhân rộng nó theo hệ số 2, diện tích của nó tăng theo hệ số 22= .

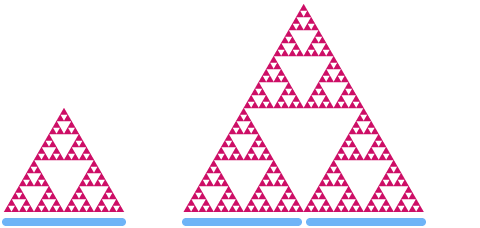
Một khối lập phương có kích thước . Khi chia tỷ lệ theo hệ số 2, khối lượng của nó tăng theo hệ số 23= . Lưu ý rằng khối lớn hơn trong hình ảnh bao gồm 8 bản sao của bản nhỏ hơn!

Bây giờ hãy để một cái nhìn về tam giác Sierpinki. Nếu chúng tôi chia tỷ lệ theo hệ số 2, bạn có thể thấy rằng phạm vi của khu vực của bạn tăng theo hệ số .

Hãy nói rằng d là kích thước của tam giác Sierpinki. Sử dụng cùng một mẫu như trên, chúng tôi nhận được 2d=3. Nói cách khác, d = 1.585 tựa

Nhưng chờ đợi, làm thế nào một cái gì đó có một thứ nguyên không phải là một số nguyên? Có vẻ như không thể, nhưng đây chỉ là một trong những tính chất kỳ lạ của fractals. Trên thực tế, đây là những gì mang lại cho fractals tên của chúng: chúng có kích thước phân đoạn.

Với mỗi lần lặp lại, chúng tôi loại bỏ một phần diện tích của tam giác Sierpinki. Nếu chúng ta có thể làm điều này vô cùng nhiều lần, thì thực sự sẽ không còn khu vực nào nữa: đó là lý do tại sao tam giác Sierpinki là một thứ gì đó nằm giữa khu vực 2 chiều và đường 1 chiều.

Trong khi nhiều fractals là tự tương tự, một định nghĩa tốt hơn là fractals là các hình có kích thước không nguyên {{}}__.

Bông tuyết Koch

Có rất nhiều hình dạng trong tự nhiên trông giống như fractals. Chúng tôi đã thấy một số nhà máy ở đầu chương này. Các ví dụ tuyệt vời khác là bông tuyết và tinh thể băng:

Để tạo ra bông tuyết fractal của riêng chúng ta, một lần nữa chúng ta phải tìm một quy trình đơn giản mà chúng ta có thể áp dụng nhiều lần.

Giống như tam giác Sierpinki, hãy bắt đầu với một tam giác đều, bằng nhau. Tuy nhiên, thay vì loại bỏ hình tam giác nhỏ hơn ở mỗi bước, chúng tôi thêm hình tam giác nhỏ hơn dọc theo cạnh. Độ dài cạnh của mỗi tam giác là của các tam giác ở bước trước.

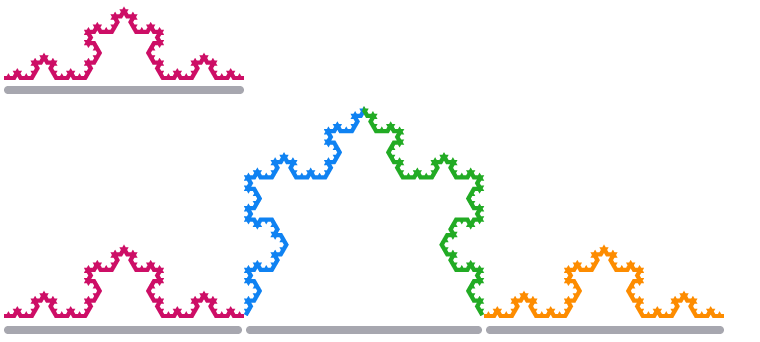
Hình dạng kết quả được gọi là Bông tuyết Koch, được đặt theo tên của nhà toán học Thụy Điển Helge von Koch. Lưu ý, một lần nữa, phần nhỏ của cạnh của bông tuyết trông giống hệt như phần lớn hơn.

Khi chúng tôi chia tỷ lệ một phân đoạn cạnh của Bông tuyết Koch theo hệ số 3, chiều dài của nó là .

Sử dụng cùng một mối quan hệ giữa các kích thước và các yếu tố tỷ lệ như trên, chúng ta có phương trình . Điều này có nghĩa là kích thước của Bông tuyết Koch là d=log34≈1.262.

Khu vực

Tạo các bông tuyết Koch gần giống như một chuỗi đệ quy: chúng ta biết hình dạng bắt đầu (một hình tam giác) và chúng ta biết cách chuyển từ một thuật ngữ này sang thuật ngữ tiếp theo (bằng cách thêm nhiều hình tam giác ở mỗi cạnh):

hình tam giác mới

Sau lần lặp đầu tiên, số lượng tam giác mới được thêm vào tăng theo hệ số ở mỗi bước. Đồng thời, diện tích của các hình tam giác mới này giảm theo hệ số ở mỗi bước.

Hãy để nói rằng tam giác đầu tiên có diện tích là 1. Sau đó, tổng diện tích của ba tam giác tiếp theo là 3×19=13. Tất cả các bước sau đây tạo thành một chuỗi hình , với tỷ lệ chung .

Sử dụng công thức tính tổng của chuỗi hình học vô hạn, chúng ta có thể tính được rằng tổng diện tích của bông tuyết Koch là

A=1+13×1=85=1.6.

Chu vi

Chúng ta cũng có thể thử tính chu vi của bông tuyết Koch. Như chúng ta đã thấy trước đây, độ dài của chu vi thay đổi theo hệ số ở mỗi bước.

Điều này có nghĩa là, một lần nữa, chúng ta có một chuỗi hình học - nhưng trong trường hợp này, nó . Điều này có nghĩa là chu vi của bông tuyết Koch thực sự là dài vô hạn!

Nếu điều này có vẻ trái ngược, chỉ cần nhớ rằng chúng tôi nhân chu vi với 43 ở mỗi bước và chúng tôi thực hiện việc này vô cùng nhiều lần.

Gần như không thể tưởng tượng rằng bạn có thể có hình dạng với diện tích hữu hạn và chu vi_ vô hạn_ - nhưng đây chỉ là một trong nhiều đặc tính bất ngờ của fractals.

Bạn có thể đưa ra bất kỳ cách nào khác để tạo ra fractals của riêng bạn?

Linh hồn của tôi đang xoắn ốc trên những mảnh nhỏ bị đóng băng xung quanh

Miếng bọt biển

Fractals don lồng phải là loại phẳng phẳng, giống như nhiều ví dụ ở trên. Một trong những mảnh nhỏ nổi tiếng nhất có hình 3 chiều là miếng bọt biển Menger, được đặt theo tên của nhà toán học Karl Menger, người đầu tiên mô tả nó vào năm 1926.

Chúng tôi bắt đầu với một khối lập phương vững chắc, và liên tục khoan các lỗ nhỏ hơn và nhỏ hơn vào các cạnh của nó. Mỗi lần lặp lỗ mới có chiều rộng của lần lặp lỗ trước đó.

Một khối 3×3×3 bao gồm 27 khối nhỏ hơn, nhưng ở đây chúng tôi đã loại bỏ một số trong số này. Miếng bọt biển Menger bao gồm]] 20]] bản sao của nó, nhỏ hơn 3 lần.

Bây giờ chúng ta có thể thử tính kích thước d của miếng bọt biển Menger giống như chúng ta đã làm cho bông tuyết Koch ở trên. Trong trường hợp này, chúng tôi nhận được 3d=20 hoặc d=log320≈2.727.

Nếu bạn tưởng tượng việc cắt ra càng nhiều lỗ, vô cùng nhiều lần, sẽ không còn khối lượng thực tế. Đó là lý do tại sao khối lập phương là không phải là 3 chiều!

Đường bờ biển Fractal

Một trong những đặc điểm chính của tất cả các fractals mà chúng tôi đã thấy cho đến nay là bạn có thể phóng to phóng to mãi mãi và luôn tìm thấy các mẫu mới. Khoảng năm 1920, nhà toán học người Anh Lewis Fry Richardson nhận ra rằng điều tương tự cũng đúng với biên giới hoặc bờ biển của nhiều quốc gia.

Bạn bắt đầu với hình dạng cơ bản của đất nước, và khi bạn phóng to, bạn thêm các cửa sông, vịnh và cửa sông, sau đó là các vách đá, đá, sỏi, v.v.

Đây là một vấn đề quan trọng khi cố gắng tính chiều dài biên giới của một quốc gia - làm thế nào để bạn quyết định phóng to bao xa, và bao gồm các ngõ ngách?

Chẳng hạn, một cách chúng ta có thể đo chiều dài bờ biển của Anh, là lấy một cây thước dài, đi bộ khắp các bãi biển của nó, và sau đó cộng tất cả các khoảng cách.

Nếu thước dài ${rulers[index]} km, chúng ta phải sử dụng ${count} lần, do đó, chúng ta có tổng đường bờ biển là ${count} × ${rulers[index]} = ${count * rulers[index]} km.

Chúng ta chỉ có thể tiếp tục, với những người cai trị nhỏ hơn và nhỏ hơn, và mỗi lần kết quả của chúng ta cho chiều dài của đường bờ biển sẽ dài hơn một chút. Giống như Bông tuyết Koch trước đây, dường như bờ biển nước Anh dài vô tận! Điều này thường được gọi là nghịch lý bờ biển.

Vài thập kỷ sau, nhà toán học Benoit Mandelbrot tình cờ bắt gặp công việc của Richardson trong một cuốn sách thư viện bị loại bỏ, khi làm việc tại IBM. Ông đã nhận ra tầm quan trọng của nó, và cũng là cách nó liên quan đến nghiên cứu gần đây hơn về fractals và kích thước.

Đường bờ biển của Anh chắc chắn có vẻ như fractal, nhưng nó không giống với _>>>>, giống như các fractals khác mà chúng tôi đã thấy trước đây. Để tìm kích thước của nó, chúng ta có thể vẽ nó trên một lưới và đếm số lượng ô mà nó giao nhau.

Ban đầu, có 88 các ô giao nhau. Nếu chúng ta chia tỷ lệ đường bờ biển theo hệ số 2, có 197 các ô giao nhau - nhiều hơn gấp đôi!

Kích thước của đường bờ biển đã tăng theo hệ số 19788. Giống như trước đây, điều này có nghĩa là kích thước của đường bờ biển là

d=log219788≈1.16

Nếu chúng ta lặp lại điều này với các lưới lớn hơn, chúng ta sẽ thấy rằng kích thước của bờ biển Anh Làn thực sự là khoảng 1,21. Mandelbrot nhận ra rằng kích thước fractal này cũng là thước đo độ nhám của một hình dạng - một khái niệm mới, mà ông đã tìm thấy các ứng dụng quan trọng trong nhiều lĩnh vực khác của toán học và khoa học.

Thêm Fractals trong tự nhiên và công nghệ

Mặc dù fractals thực sự không bao giờ có thể xuất hiện trong tự nhiên, có rất nhiều đối tượng trông giống như gần như giống như fractals. Chúng tôi đã nhìn thấy thực vật, bông tuyết và bờ biển, và đây là một số ví dụ khác:

Dãy núi ở Trung Á

Đồng bằng sông Hằng ở Ấn Độ

tia sét

Mạch máu ở võng mạc

Grand Canyon ở Hoa Kỳ

Mây

Tất cả các đối tượng này có thể xuất hiện hoàn toàn ngẫu nhiên, nhưng, giống như fractals, có một mô hình cơ bản xác định cách chúng được hình thành. Toán học có thể giúp chúng ta hiểu các hình dạng tốt hơn và fractals có các ứng dụng trong các lĩnh vực như y học, sinh học, địa chất và khí tượng.

Địa hình fractal do máy tính tạo ra

Ví dụ, chúng ta cũng có thể sử dụng các hình nhỏ để tạo ra các bản sao thực tế, bản chất, như phong cảnh và kết cấu được sử dụng trong các trò chơi video hoặc phim do máy tính tạo ra. Nước, núi và mây trong hình ảnh này được tạo ra hoàn toàn bằng máy tính, với sự trợ giúp của fractals!

Và chúng tôi thậm chí có thể đảo ngược quá trình này để nén hình ảnh kỹ thuật số, để giảm kích thước tệp của chúng. Các thuật toán đầu tiên được phát triển bởi Michael Barnsley và Alan Sloan vào những năm 1980, và những thuật toán mới vẫn đang được nghiên cứu cho đến ngày nay.

Thay đổi ngôn ngữ

Đăng nhập Mathigon

Chia sẻ

Đặt lại tiến độ

Bảng chú giải