Biến đổi và đối xứngNhóm đối xứng và hình nền
Một số hình có nhiều hơn một đối xứng - hãy xem








Bạn đã chỉ ra ở trên rằng một hình vuông có
Nó cũng có tính đối xứng quay
Và cuối cùng, chúng ta có thể nghĩ về việc không làm gì khác như một kiểu đối xứng đặc biệt khác - bởi vì kết quả là (rõ ràng) giống như trước đây. Điều này đôi khi được gọi là danh tính .
Tổng cộng, chúng tôi đã tìm thấy
Bây giờ chúng ta thực sự có thể bắt đầu thực hiện một số số học với các đối xứng này. Ví dụ: chúng ta có thể thêm hai đối xứng để có được những đối xứng mới:






Bất cứ khi nào bạn thêm hai đối xứng của một hình vuông, bạn sẽ có một hình mới. Đây là một máy tính đối xứng của người Viking, nơi bạn có thể tự mình thử:
Dành thời gian chơi xung quanh với máy tính đối xứng và cố gắng tìm bất kỳ mẫu nào. Bạn có thể hoàn thành những quan sát này?
- Thêm hai phép quay sẽ luôn cho
(hoặc bản sắc). * Thêm hai phản xạ sẽ luôn luôn cho (hoặc bản sắc). * Thêm hai đối xứng giống nhau theo thứ tự ngược lại kết quả * Thêm danh tính .
Bạn có thể đã nhận ra rằng thêm đối xứng thực sự rất giống với việc thêm số nguyên :
- Adding two symmetries/integers always gives another symmetry/integer:
+ = 12 + 7 = 19 - Adding symmetries/integers is
associative :+ + = + + 4 + 2 + 5 = 4 + 2 + 5 - Every symmetry/integer has an inverse, another symmetry/integer which, when added, gives the identity:
+ = 4 + –4 = 0
Trong toán học, bất kỳ bộ sưu tập nào có các tính chất này được gọi là một
Trong ví dụ này, chúng tôi bắt đầu với tám đối xứng của hình vuông. Trong thực tế, mỗi hình dạng hình học có nhóm đối xứng riêng. Chúng đều có các yếu tố khác nhau, nhưng chúng luôn đáp ứng ba quy tắc trên.
Các nhóm xuất hiện ở mọi nơi trong toán học. Các phần tử có thể là số hoặc đối xứng, nhưng cũng là đa thức, hoán vị, ma trận, hàm số bất cứ thứ gì tuân theo ba quy tắc. Ý tưởng chính của lý thuyết nhóm là chúng ta không quan tâm đến các yếu tố riêng lẻ, chỉ là cách chúng tương tác với nhau .
Ví dụ, các nhóm đối xứng của các phân tử khác nhau có thể giúp các nhà khoa học dự đoán và giải thích các tính chất của các vật liệu tương ứng.
Các nhóm cũng có thể được sử dụng để phân tích chiến lược chiến thắng trong các trò chơi trên bàn cờ, hành vi của virus trong y học, các hòa âm khác nhau trong âm nhạc và nhiều khái niệm khác.
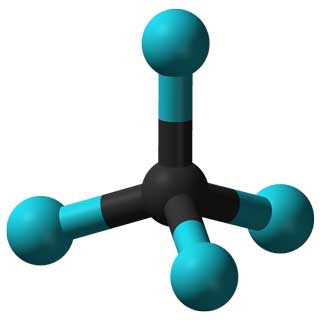
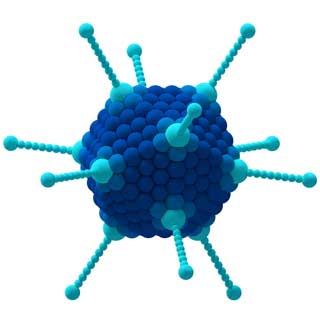
Các thuộc tính của phân tử CCl 4 (trái) và Adenovirus (phải) được xác định bởi các đối xứng của chúng.
Nhóm hình nền
Trong các phần trước chúng ta đã thấy hai loại đối xứng khác nhau tương ứng với hai phép biến đổi khác nhau: phép quay và phản xạ. Nhưng cũng có một sự đối xứng cho loại chuyển đổi cứng nhắc thứ ba:


Honyecomb lục giác


Gạch ốp tường
Ngoài đối xứng phản xạ, quay và đối xứng, thậm chí còn có một loại thứ tư:


Một mẫu có thể có nhiều hơn một loại đối xứng. Và cũng giống như đối với hình vuông, chúng ta có thể tìm thấy
Các nhóm này không cho bạn biết nhiều về hình mẫu trông như thế nào (ví dụ như màu sắc và hình dạng của nó), chỉ là cách nó được lặp lại . Nhiều mẫu khác nhau có thể có cùng một nhóm đối xứng - miễn là được sắp xếp và lặp lại theo cùng một cách.


Hai mẫu này có cùng tính đối xứng, mặc dù chúng trông rất khác nhau. Nhưng đối xứng không phải là về màu sắc, hoặc hình dạng bề ngoài.


Hai mẫu này cũng có các đối xứng giống nhau - mặc dù chúng trông giống với các mẫu tương ứng ở bên trái, hơn là với nhau.
Nó chỉ ra rằng, trong khi có vô số các mẫu có thể, tất cả chúng đều có một trong số 17 nhóm đối xứng khác nhau. Chúng được gọi là Nhóm hình nền . Mỗi nhóm hình nền được xác định bởi sự kết hợp của các bản dịch, xoay, phản xạ và phản xạ trượt. Bạn có thể thấy các

Group 1 – P1
Only translations div img(src="/content/transformations/images/wallpapers/p2.svg" width=360, height=240) p.caption Group 2 – P2 Rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/p3.svg" width=360, height=240) p.caption Group 3 – P3 Rotations of order 3 (120°), translations div img(src="/content/transformations/images/wallpapers/p4.svg" width=360, height=240) p.caption Group 4 – P4 Four rotations of order 2 (180°), translations div img(src="/content/transformations/images/wallpapers/p6.svg" width=360, height=240) p.caption Group 5 – P6 Rotations of order 2, 3 and 6 (60°), translations div img(src="/content/transformations/images/wallpapers/pm.svg" width=360, height=240) p.caption Group 6 – PM Parallel axes of reflection, translations div img(src="/content/transformations/images/wallpapers/pmm.svg" width=360, height=240) p.caption Group 7 – PMM Perpendicular reflections, rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/p4m.svg" width=360, height=240) p.caption Group 8 – P4M Rotations (ord 2 + 4), reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p6m.svg" width=360, height=240) p.caption Group 9 – P6M Rotations (ord 2 + 6), reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p3m1.svg" width=360, height=240) p.caption Group 10 – P3M1 Rotations of order 3, reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p31m.svg" width=360, height=240) p.caption Group 11 – P31M Rotations of order 3, reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p4g.svg" width=360, height=240) p.caption Group 12 – P4G Rotations (ord 2 + 4), reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/cmm.svg" width=360, height=240) p.caption Group 13 – CMM Perpendicular reflections, rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/pmg.svg" width=360, height=240) p.caption Group 14 – PMG Reflections, glide reflections, rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/pg.svg" width=360, height=240) p.caption Group 15 – PG Parallel glide reflections, translations div img(src="/content/transformations/images/wallpapers/cm.svg" width=360, height=240) p.caption Group 16 – CM Reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/pgg.svg" width=360, height=240) p.caption Group 17 – PGG Perpendicular glide reflections, rotations of order 2, translations
Thật không may, không có lý do đơn giản tại sao có 17 nhóm này, và chứng minh nó đòi hỏi toán học tiên tiến hơn. Thay vào đó, bạn có thể thử vẽ các mẫu lặp lại của riêng mình cho mỗi trong số 17 nhóm hình nền:
Examples of other students’ drawings



Các nhóm hình nền là tất cả về mô hình hai chiều phẳng. Chúng ta có thể làm một cái gì đó tương tự cho các mô hình ba chiều: chúng được gọi là các nhóm tinh thể học, và có 219 trong số chúng!
Ngoài các bản dịch, phản xạ, xoay và phản xạ trượt, các nhóm này bao gồm các đối xứng như mặt phẳng trượt và trục vít (nghĩ về chuyển động khi tháo nắp chai).
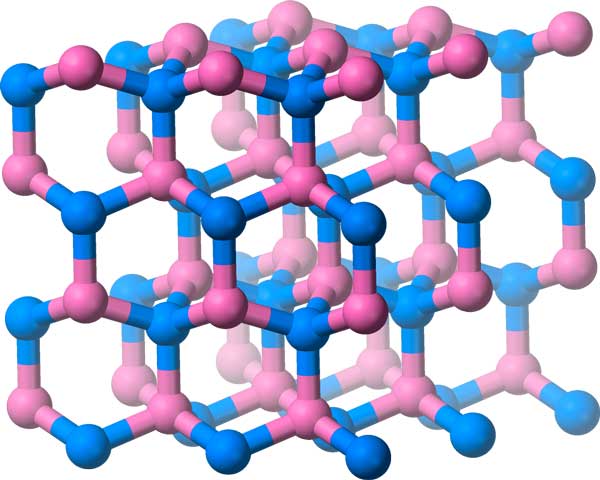
Boron-Nitride có các phân tử được sắp xếp trong mạng tinh thể này, có nhóm đối xứng ba chiều.