Đa giác và đa diệnTessellations

Đa giác xuất hiện ở mọi nơi trong tự nhiên. Chúng đặc biệt hữu ích nếu bạn muốn xếp một khu vực rộng lớn, bởi vì bạn có thể ghép các đa giác lại với nhau mà không có bất kỳ khoảng trống hoặc chồng chéo nào. Các mô hình như thế được gọi là tessellations .

Tổ ong

Sinaloan Sữa rắn da

Cấu trúc tế bào của lá

Cột bazan tại Giant 'Causeway ở Bắc Ireland

Da dứa

Vỏ rùa

Con người đã sao chép nhiều mô hình tự nhiên này trong nghệ thuật, kiến trúc và công nghệ - từ thời La Mã cổ đại cho đến hiện tại. Đây là vài ví dụ:

Mô hình vỉa hè hình

Nhà kính tại Dự án Eden ở Anh

Khảm tại Alhambra

Mái nhà hình tại Bảo tàng Anh ở London

Gian hàng tessname di động ở Sydney

Nghiên cứu về sự phân chia thường xuyên của máy bay với bò sát , MC Escher

Tại đây bạn có thể tạo các tessellations của riêng mình bằng cách sử dụng đa giác thông thường. Chỉ cần kéo hình dạng mới từ thanh bên vào khung vẽ. Những hình dạng tessellate tốt? Có hình dạng nào không tessellate không? Cố gắng tạo ra các mô hình thú vị!

Examples of other students’ tessellations

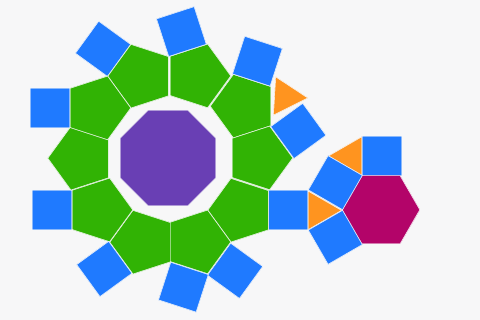
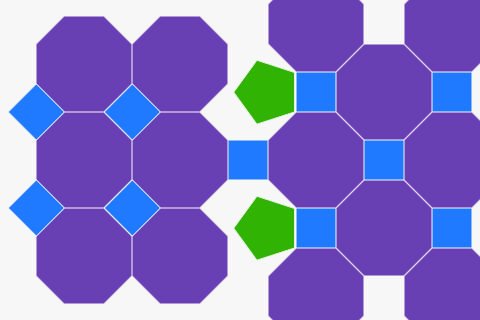
Tessellations từ đa giác thông thường

Bạn có thể nhận thấy rằng một số đa giác thông thường (như ) tessellate rất dễ dàng, trong khi những người khác (như ) dường như không tessellate.

Điều này có liên quan đến kích thước của các góc bên trong của chúng, mà chúng ta đã học cách tính toán trước đó. Tại mọi đỉnh trong phần tử, các góc bên trong của nhiều đa giác khác nhau gặp nhau. Chúng ta cần tất cả các góc này để thêm tới °, nếu không sẽ có một khoảng cách hoặc chồng chéo.

Tam giác vì 6 × 60° = 360°.

Hình vuông vì 4 × 90° = 360°.

Ngũ giác bởi vì bội số của 108° không thêm tới 360°.

Lục giác vì 3 × 120° = 360°.

Bạn có thể kiểm tra tương tự rằng, giống như các hình ngũ giác, bất kỳ đa giác thông thường nào có 7 cạnh trở lên không bị xé. Điều này có nghĩa là các đa giác thông thường duy nhất mà tessellate là hình tam giác, hình vuông và hình lục giác!

Tất nhiên, bạn có thể kết hợp các loại đa giác thông thường khác nhau trong một phần tử, với điều kiện là các góc bên trong của chúng có thể tăng tới 360°:

Squares and triangles
90° + 90° + 60° + 60° + 60° = 360°

Hexagons and triangles
120° + 120° + 60° + 60° = 360°

Hexagons and triangles
120° + 60° + 60° + 60° + 60° = 360°

Hexagons, squares and triangles
120° + 90° + 90° + 60° = 360°

Octagons and squares
135° + 135° + 90° = 360°

Dodecagons (12-gons) and triangles
150° + 150° + 60° = 360°

Dodecagons, hexagons and squares
150° + 120° + 90° = 360°

Tessellations từ đa giác bất thường

Chúng ta cũng có thể thử tạo ra các phần tử từ các đa giác không đều - miễn là chúng ta cẩn thận khi xoay và sắp xếp chúng.

Nó chỉ ra rằng bạn có thể tessellate không chỉ là tam giác đều, mà bất kỳ tam giác ! Hãy thử di chuyển các đỉnh trong sơ đồ này.

Tổng các góc trong một tam giác là °. Nếu chúng ta sử dụng mỗi góc ở mỗi đỉnh trong phần thứ ba, chúng ta nhận được 360°:

Đáng ngạc nhiên hơn, bất kỳ tứ giác cũng tessellates! Tổng góc bên trong của chúng là °, vì vậy nếu chúng ta sử dụng mỗi góc ở mỗi đỉnh trong phần thứ ba, chúng ta có 360°.

Ngũ giác là một chút phức tạp hơn. Chúng ta đã thấy rằng các hình ngũ giác đều đặn , nhưng những người không thường xuyên?

Dưới đây là ba ví dụ khác nhau về các tessellations với ngũ giác. Chúng không thường xuyên , nhưng chúng là đa giác 5 mặt hoàn toàn hợp lệ.

Cho đến nay, các nhà toán học chỉ tìm thấy 15 loại khác nhau với các hình ngũ giác (lồi) - loại gần đây nhất được phát hiện vào năm 2015. Không ai biết liệu có loại nào khác không, hoặc nếu 15 loại này là những loại duy nhất

Tessellations trong nghệ thuật

Tessellations chúng tôi vừa là công cụ vừa là nguồn cảm hứng cho nhiều nghệ sĩ, kiến trúc sư và nhà thiết kế - nổi tiếng nhất là nghệ sĩ người Hà Lan MC Escher . Tác phẩm của Escher chứa những sinh vật, mô hình và phong cảnh kỳ lạ, đột biến:

“Sky and Water I” (1938)

“Lizard” (1942)

“Lizard, Fish, Bat” (1952)

“Butterfly” (1948)

“Two Fish” (1942)

“Shells and Starfish” (1941)

Những tác phẩm nghệ thuật này thường trông vui nhộn và dễ dàng, nhưng các nguyên tắc toán học cơ bản vẫn giống như trước: góc, góc quay, bản dịch và đa giác. Nếu toán học không đúng, thì tessname sẽ không hoạt động!

“Metamorphosis II” by M. C. Escher (1940)

Penrose

Tất cả các điều mà chúng ta thấy cho đến nay đều có một điểm chung: chúng là định kỳ . Điều đó có nghĩa là chúng bao gồm một mô hình thông thường được lặp đi lặp lại nhiều lần. Chúng có thể tiếp tục mãi mãi theo mọi hướng và chúng sẽ trông giống nhau ở mọi nơi.

Vào những năm 1970, nhà toán học và vật lý học người Anh Roger Penrose đã phát hiện ra những câu chuyện không định kỳ - chúng vẫn tiếp tục vô tận theo mọi hướng, nhưng không bao giờ giống hệt nhau. Chúng được gọi là nghiêng Penrose và bạn chỉ cần một vài loại đa giác khác nhau để tạo một:

Move the slider to reveal the underlying structure of this tessellation. Notice how you have the same patterns at various scales: the small yellow pentagons, blue stars, orange rhombi and green ‘ships’ appear in their original size, in a slightly larger size and an even larger size. This self-similarity can be used to prove that this Penrose tiling is non-periodic.

Penrose đã khám phá các tessellations hoàn toàn cho vui, nhưng hóa ra cấu trúc bên trong của một số vật liệu thực (như nhôm) theo một mô hình tương tự. Mẫu này thậm chí còn được sử dụng trên giấy vệ sinh, bởi vì các nhà sản xuất nhận thấy rằng một mẫu không định kỳ có thể được cuộn lên mà không có bất kỳ chỗ phồng nào.

Thay đổi ngôn ngữ

Đăng nhập Mathigon

Chia sẻ

Đặt lại tiến độ