Đa giác và đa diệnChất rắn Platonic

Khi bắt đầu khóa học này, chúng tôi đã định nghĩa các đa giác thông thường là các đa giác đặc biệt đối xứng trực tiếp, trong đó tất cả các cạnh và góc đều giống nhau. Chúng ta có thể làm một cái gì đó tương tự cho khối đa diện.

Trong một khối đa diện đều, tất cả các mặt đều là cùng một loại đa giác thông thường, và cùng một số mặt gặp nhau ở mọi đỉnh . Polyhedra với hai tính chất này được gọi là chất rắn Platonic , được đặt theo tên của triết gia Hy Lạp Plato .

Vì vậy, các chất rắn Platonic trông như thế nào - và có bao nhiêu trong số chúng? Để tạo hình ba chiều, chúng ta cần ít nhất mặt để gặp nhau ở mọi đỉnh. Hãy bắt đầu một cách có hệ thống với đa giác thông thường nhỏ nhất: tam giác đều:

Và bảy hoặc nhiều hình tam giác ở mọi đỉnh cũng không tạo ra các khối đa diện mới: không có đủ không gian xung quanh một đỉnh, để phù hợp với nhiều hình tam giác đó.

Điều này có nghĩa là chúng tôi đã tìm thấy chất rắn Platonic bao gồm các hình tam giác. Hãy chuyển sang đa giác thông thường tiếp theo: hình vuông.

Tiếp theo, hãy thử các hình ngũ giác đều đặn:

Nếu hình ngũ giác gặp nhau ở mọi đỉnh, chúng ta sẽ có được Dodecahedron . Nó có khuôn mặt. (Cúc Dodeca 'có nghĩa là người mười hai người Viking trong tiếng Hy Lạp.)

Đa giác thông thường tiếp theo để thử là hình lục giác:

Nếu ba hình lục giác gặp nhau tại mỗi đỉnh, chúng tôi ngay lập tức nhận được một tessellation khối đa diện khối sáu mặt . Vì không có không gian cho hơn ba, nên có vẻ như không có chất rắn Platonic bao gồm các hình lục giác.

Điều tương tự cũng xảy ra đối với tất cả các đa giác thông thường có nhiều hơn sáu mặt. Họ không tessellate, và chúng tôi chắc chắn không nhận được bất kỳ đa giác ba chiều.

Điều này có nghĩa là chỉ có chất rắn Platonic! Chúng ta hãy cùng nhau xem xét tất cả chúng:

Chú ý số lượng mặt và đỉnh được hoán đổi xung quanh tương tự đối với khối lập phương và khối tám mặt , cũng như khối mười hai mặt và icosahedron , trong khi số cạnh vẫn giữ nguyên là khác nhau Những cặp chất rắn Platonic này được gọi là chất rắn kép .

Chúng ta có thể biến một khối đa diện thành hai mặt của nó, bằng cách thay thế một mặt của mọi mặt bằng một đỉnh và mọi đỉnh bằng một mặt. Những hình ảnh động này cho thấy:

Tứ diện là kép với chính nó. Vì nó có cùng số mặt và đỉnh, nên việc hoán đổi chúng sẽ không thay đổi gì cả.

Plato tin rằng tất cả vật chất trong Vũ trụ bao gồm bốn yếu tố: Không khí, Trái đất, Nước và Lửa. Ông nghĩ rằng mọi nguyên tố tương ứng với một trong các chất rắn Platonic, trong khi phần tử thứ năm sẽ đại diện cho toàn bộ vũ trụ. Ngày nay chúng ta biết rằng có hơn 100 nguyên tố khác nhau bao gồm các nguyên tử hình cầu, không phải khối đa diện.

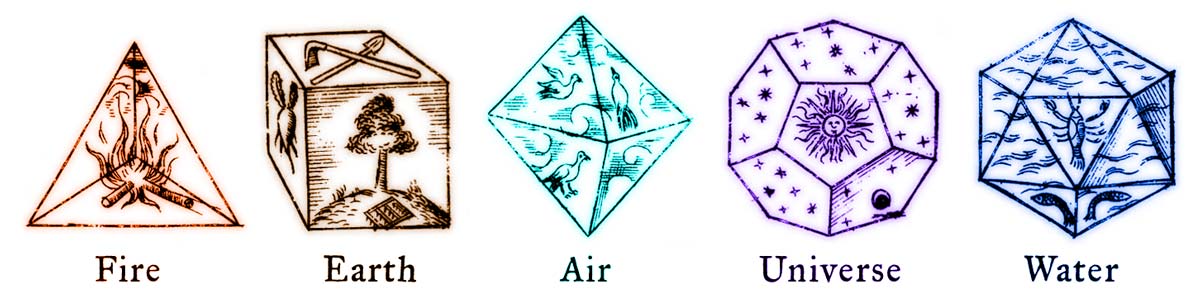
Images from Johannes Kepler’s book “Harmonices Mundi” (1619)

Chất rắn Archimedean

Chất rắn Platonic là khối đa diện đặc biệt quan trọng, nhưng có vô số khác.

Các chất rắn Archimedean , ví dụ, vẫn phải được tạo thành từ các đa giác thông thường , nhưng bạn có thể sử dụng nhiều loại khác nhau. Chúng được đặt theo tên của một nhà toán học Hy Lạp khác, Archimedes of Syracuse , và có 13 người trong số họ:

Các ứng dụng

Plato đã sai khi tin rằng tất cả các nguyên tố bao gồm chất rắn Platonic. Nhưng khối đa diện thông thường có nhiều tính chất đặc biệt khiến chúng xuất hiện ở nơi khác trong tự nhiên - và chúng ta có thể sao chép các tính chất này trong khoa học và kỹ thuật.